Given the equation
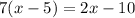
First step solve the term in the parenthesis by applying the distributive propperty of mutiplication that states that if you have a(b+c)→ab+ac
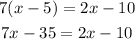
Next pass all x-related terms to one side of the equation and the others to the other side:
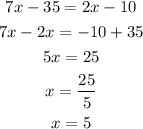
x=5