Quadratic Function
We are given the function
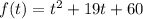
1) Find the zeros of the function
The zeros or roots of f, are found by equating it to 0:

The standard representation of a quadratic function is:

where a,b, and c are constants.
Solving with the quadratic formula:

The coefficients can be established by comparing the generic equation with the given equation, thus: a=1, b=19, c=60. Substituting:
![\displaystyle t=\frac{-19\pm\sqrt[]{19^2-4(1)(60)}}{2(1)}=\frac{-19\pm\sqrt[]{361-240}}{2}=\frac{-19\pm\sqrt[]{121}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/s7v1krji70u7r4cm6zkx9wrwybfjtohun0.png)
Operating:
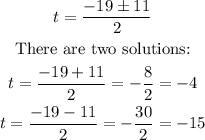
The smaller root is -15, the larger root is -4. Answer:
-15
-4
2) The quadratic equation can be also written in vertex form:
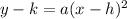
Where a is the leading coefficient and (h,k) is the vertex.
To find this form, we need to complete squares as follows.
We need to recall this identity:
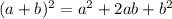
Comparing the given function, we can see the first term is t=a, the second term should be 2ab=19t, thus b=19/2
To complete the square, we need to add and subtract b^2 as follows:
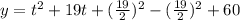
Now we apply the identity:
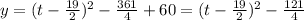
Finally, we add 121/4:

Comparing with the vertex form of the quadratic function:
a=1
Vertex: (19/2,-121/4)