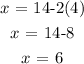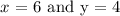
Here, we want to solve the system of linear equations simultaneously
We can start by getting an expression for x from the second equation
We have this as;
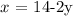
We proceed to substitute this into the first equation
We have this as;
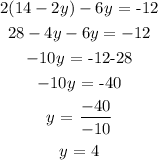
To get the value of x, we simply substitute the y-value into the equation for x
We have this as;