Question

with one method of a procedure called acceptance sampling a sample of items is randomly selected without replacement and the entire batch is accepted if every item is in the sample is okay a company is just manufactured 1,938 CDs and 316 are defective A) if there are 316 defective CDs then that means there were ___ good CDs produced B) what is the probability that all 4 CDs are good if you are selecting without replacement C) now in certain circumstances we can use the 5% guideline for cumbersome calculations to treat events that are really dependent as independent instead so that calculations are easier and this problem here can we implement the 5% guideline? A. No, because 4 CDs chosen out of 1938 is not less than 5% B. yes, because 4 CDs chosen out of 1938 is more than 5%C. yes, because four CDs chosen out of 1938 is less than 5%D. no, because 316 defective CDs out of 1938 is not less than 5%E. no, because 1,622 good CDs out of 1938 is not less than 5%D) assuming that you can treat this situation as independent disregarding your answer to part C to utilize that 5% guideline what is the probability that all 4 CDs are good? E) assuming that you can treat the situation as independent regardless of your answer for part C which of the answers above part D or part B is the best to use? A. answer choice D is best because sampling with the replacement is the most effective way to conduct acceptance samplingB. answer choice DS best to use because the 5% guideline is very accurateC. answer choice B is the best because part D was calculated with the 5% guideline meaning it is just an estimateD. is your choice B is best because it utilizes the 5% guideline

Answer 1

Since we have that 316 CDs are defective from 1938, then:

`1938─316=1622`

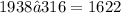
A) we have that 1622 good CDs were produced.

B) If A is the probability that all 4 cds are good if you are selecting without replacement is:

`\begin{gathered} P(A)=((1622)/(1938))((1621)/(1937))((1622)/(1936))((1619)/(1935))=0.490372393 \\ P(A)=0.4904 \end{gathered}`

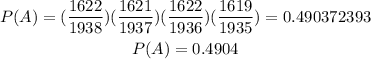
C)In this case, we can use the 5% guideline, since the sample size is 4 and it's less than the 5% of 1938 (option C).

D) We can check this by calculating the probability assuming each selection is with replacement:

`\begin{gathered} P(A)=((1622)/(1938))^4=0.490668648 \\ P(A)=0.4907 \end{gathered}`

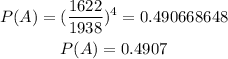
Then, the probability that all 4 CDs are good assuming this situation is independent is 0.4907

E)We have seen that both probabilities are almost the same, but in most cases, it's best to use the 5% guideline. Therefore, the answer D is the best choise because the 5% guideline is very accurate in this case (otpion B)