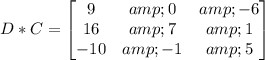With the given matrices, we need to solve the next operations:
A*B =
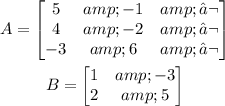
To multiply two matrices, A needs to have the same number of columns as the number of rows for B.
Then, A is a matrix 3x2
B is a matrix 2x2
Now, we need to multiply columns by rows:
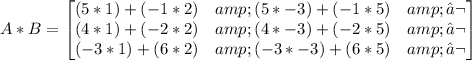
Simplify
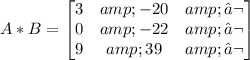
Now, let us find 2B + C
First, let us find 2B:
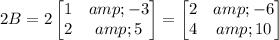
Now, we need to find 2B + C. However, to add up to two matrices they must have the same number of rows and columns.
Therefore, it is not possible to do 2B + C.
3A- D =
Let us find 3A
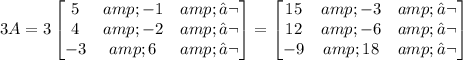
Now, we can subtract D:
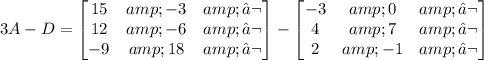
Then:
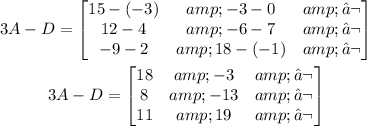
Finally, let us find D*C=
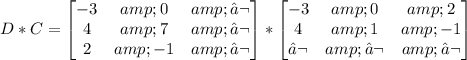
It is possible to multiply both matrices because the number of columns for D is equal to the number of rows for C.
Then:
![D\ast C=\begin{bmatrix}{(-3\ast-3)+(0\operatorname{\ast}4)} & {(-3\operatorname{\ast}0)+(0\operatorname{\ast}1)} & {(-3\operatorname{\ast}2)+(0\operatorname{\ast}-1)} \\ {(4\operatorname{\ast}-3)+(7\operatorname{\ast}4)} & {(4\operatorname{\ast}0)+(7\operatorname{\ast}1)} & {(4\operatorname{\ast}2)+(7\operatorname{\ast}-1)} \\ {(2\operatorname{\ast}-3)+(-1\operatorname{\ast}4)} & {(2\operatorname{\ast}0)+(-1\operatorname{\ast}1)} & {(2\operatorname{\ast}2)+(-1\operatorname{\ast}-2)}\end{bmatrix}]()
Simplify the operations. Then: