Question

Today you have exactly $600.38 in your savings account earning exactly 0.5% interest, compounded monthly. How many years will it take before that account reaches $1030.14? Use trial and error to find the number of years (t). Explain how you know your answer is correct.

Answer 1

`107.9\text{ years}`

Step-by-step explanation

To find the number of years before the account reaches $1030.14, we have to apply the formula for monthly compounded amount:

`A=P(1+(r)/(12))^(12t)`

where P = initial amount = $600.38

r = interest rate = 0.5% = 0.005

t = number of years

Therefore, solve for t:

`\begin{gathered} 1030.14=600.38(1+(0.005)/(12))^(12\cdot t) \\ \Rightarrow(1030.14)/(600.38)=(1.000417)^(12t) \\ \Rightarrow1.716=1.000417^(12t) \end{gathered}`

Convert the exponential equation above into a logarithmic equation as follows:

`\log _(1.000417)1.716=12t`

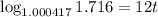
Therefore, we have that:

`\begin{gathered} (\log _(10)1.716)/(\log _(10)1.000417)=12t \\ \Rightarrow12t=1294.96 \\ t=(1294.96)/(12) \\ t\approx107.9\text{ years} \end{gathered}`

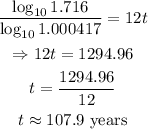
That is the number of years that it will take.