Question

Consider the function given by the graph. What are

these values?
fl-2) =
10) =
f(4) =

Answer 1

f(-2) = 2

f(0) = 4

f(4) = -1

Step-by-step explanation:

Given the graph of a piecewise function:

`\displaystyle\mathsf{f(x) = \left \{ {{x\:+\:4\quad if\:\:x\leq \:0} \atop {-(1)/(2)x\:+\:1\quad if\:\:x\: >\:0}} \right.}\\`

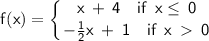
Side note:

I used the method of finding the linear equations in slope-intercept form to establish the piecewise function. First, I solved for the slope by choosing two points in each defined interval. Then, I plugged in the y-intercepts of each interval, for f(x) = x + 4: the y-intercept is (0, 4) where b = 4; for f(x) = -½x + 1, the y-intercept is (0, 1) where b = 1.

Step-by-step explanation:

There are two methods for determining the range values of the given domain values.

Method 1: The first method is using the graph to find the corresponding range values of the given domain {-2, 0, 4}.

Method 2: Alternatively, we could use the rules provided by the piecewise function in evaluating the following domain values. This post will use the second method (using the piecewise function) to evaluate the input values.

Regardless of the method used, the results will remain the same.

f(-2)

Since the input value is x = -2, then we must use the function, f(x) = x + 4:

f(x) = x + 4

f(-2) = -2 + 4

f(-2) = 2

Therefore, the range value given the domain, x = -2 is 2, or simply: f(-2) = 2.

f(0)

Given the input value is x = 0, then we must also use the function, f(x) = x + 4:

f(x) = x + 4

f(0) = 0 + 4

f(0) = 4

Therefore, the range value given the domain, x = 0 is 4, or f(0) = 4.

f(4)

Since the input value is x = 4, then we must use the function, f(x) = -½x + 1:

f(x) = -½x + 1

f(4) = -½(4) + 1

f(4) = -2 + 1

f(4) = -1

Therefore, the range value given the domain, x = 4 is -1, or f(4) = -1.