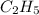The question requires us to obtain the empirical formula for a hydrocarbon that is composed of 4.8g of carbon and 1.0g of hydrogen.
To solve this problem, we'll need to go through the following steps:
1) Find the percentage of each element in the hydrocarbon, considering the masses given;
2) Consider a sample with 100g of the hydrocarbon and calculate the number of moles of C and H that would be in this sample;
3) Find a whole-number ratio by dividing the moles of each element by whichever of the moles from step 2 is the smallest
4) Work with the coefficients found in step 3 to write the empirical formula
Next, we'll go through these steps to solve the probem:
1) Considering the values given, we can calculate the percentages of C and H in the molecule:
sample = 4.8 g of C + 1.0 g of H = 5.8 g total (100%)
total mass = 5.8 g ---------------- 100%
mass of C = 4.8 g ---------------- x = 82.75% (percentage of C)
total mass = 5.8 g ---------------- 100%
mass of H = 1.0 g ---------------- x = 17.25% (percentage of H)
2) Now that we know the percentage of each element, we can calculate the number of moles of each one considering a 100 g sample (this sample would have 82.75g of C and 17.25g of H). The atomic masses are 12.01 u for C and 1.01 u for H.
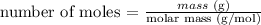
number of moles for C = 82.75 g / 12.01 g/mol = 6.89 mol
number of moles for H = 17.25 g / 1.01 g/mol = 17.08 mol
3) Next, we divide the values obtained in step 2 by the smallest value obtained, in order to find a whole-number ratio:
C = 6.89 / 6.89 = 1.00
H = 17.08 / 6.89 = 2.48
4) The values found in step 3 can be used to write a chemical formula (still with non integer numbers):
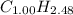
Now, we need to find the correct coefficients for the empirical formula. Note that if we multiply both coefficients by 2, we'll have an integer for C (2.00) and a number for H that can be rounded up (4.96 ≈ 5.00).
Therefore, we can write the empirical formula for this hydrocarbon as: