ANSWER
M = (4, 2)
Step-by-step explanation
We want to find the coordinates of the midpoint of the segment having endpoints T(3, 1) and U(5, 3)
We know that cordinates in 2 dimensions are given in the form:
A(x, y)
So, to find the midpoint, we have to add the two x cordinates from T and U and divide by 2 and then do the same for y.
In other words:
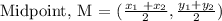
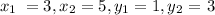
Therefore, the midpoint, M, is:
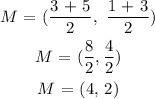
That is the midpoint