Question

Asking a question here

Answer 1

You have the following expression:

`\sqrt[]{40x^4y^3z}`

In order to simplify it you need to remember this property for Radicals:

`\sqrt[n]{a^n}=a^{(n)/(n)}=a`

Then:

- Descompose the number 40 into its Prime factors:

`40=2\cdot2\cdot2\cdot5`

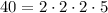
- Apply the Product of Powers property that states:

`(b^m)(b^n)=b^((m+n))`

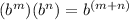
Then:

`40=2^2\cdot2\cdot5`

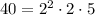
- Rewrite the expression:

`=\sqrt[]{2^2\cdot2\cdot5\cdot x^4\cdot y^2\cdot y\cdot z}`

- Simplifying, you get:

`=2x^2y\sqrt[]{2\cdot5yz}=2x^2y\sqrt[]{10yz}`

The answer is:

`2x^2y\sqrt[]{10yz}`