Question

I need help in math can you please help me

Answer 1

We are given the following trigonometric expression:

`(\sin \theta-\csc \theta)/(\cos \theta)`

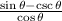
We are asked to put this expression as a function of sines and cosines, t do this, let's remember the following relationship:

`\csc \theta=(1)/(\sin \theta)`

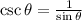
Now we replace this in the expression:

`(\sin \theta-(1)/(\sin\theta))/(\cos \theta)`

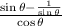
Now we do the operation in the numerator, like this:

`(((\sin\theta)(\sin\theta)-1)/(\sin\theta))/(\cos \theta)`

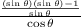
We simplify the result:

`(\sin ^2\theta-1)/(\sin \theta\cos \theta)`

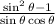
now we use the following relationship:

`\begin{gathered} \sin ^2\theta+\cos ^2\theta=1 \\ \cos ^2\theta=1-\sin ^2\theta \\ -\cos ^2\theta=\sin ^2\theta-1 \end{gathered}`

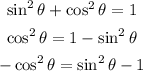
replacing this in the expression

`(-\cos ^2\theta)/(\sin \theta\cos \theta)`

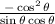
simplifying:

`-(\cos \theta)/(\sin \theta)`

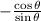
Since we are asked to put the expression as a function of sines and cosines we can't simplify any further, therefore the previous expression is the result.