Question

If EFG, E(-2,7), F(7,-8) and G(-6,-3). Is EFG a right triangle. Provide proof ofvyour yes/no answer. The use of the grid atvthe right is optional.

Answer 1

Proof of a Right Angle Triangle.

Step 1: Determine the distance between EF, FG and GE.

Using the formula below;

`\text{Distance = }\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`
`\begin{gathered} E(-2,7)\Rightarrow x_1=-2;y_1=7_{} \\ F(7,-8)\Rightarrow x_2=7;y_2=-8 \end{gathered}`
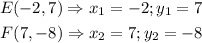
`\begin{gathered} |EF|=\sqrt[]{(7--2)^2+(-8-7)^2} \\ |EF|=\sqrt[]{9^2+(-15)^2}=\text{ }\sqrt[]{(81+225)} \\ |EF|=\sqrt[]{306}=17.493 \end{gathered}`
`\begin{gathered} F(7,-8)\Rightarrow x_1=7;y_1=-8 \\ G(-6,-3)\Rightarrow x_2=-6;y_2=-3 \end{gathered}`
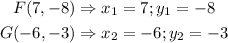
`\begin{gathered} |FG|=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ |FG|=\sqrt[]{(-6-7)^2+(-3--8)^2}=\text{ }\sqrt[]{(-13)^2+(-3+8)^2} \\ |FG|=\sqrt[]{(169+5^2}=\sqrt[]{(169+25)} \\ |FG|=\sqrt[]{194}=13.928 \end{gathered}`
`\begin{gathered} G(-6,-3)\Rightarrow x_1=-6;y_1=-3 \\ E(-2.7)\Rightarrow x_2=-2;y_2=7 \end{gathered}`
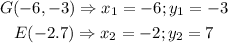
`\begin{gathered} |GE|=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ |GE|=\sqrt[]{(-2--6)^2+(7--3)^2}=\text{ }\sqrt[]{(-2+6)^2+(7+3)^2} \\ |GE|=\sqrt[]{4^2+10^2}=\sqrt[]{16+100} \\ |GE|=\sqrt[]{116}=10.770 \end{gathered}`

Step 2: If the sum of the square of two sides is equal to the square of the largest side, then we conclude that the triangle EFG is a right-angled triangle, otherwise, it is not a right-angled triangle.

That is,

`\begin{gathered} |FG|^2+|GE|^2=|EF|^2 \\ 194+116=306 \\ 310=306 \\ \text{Clearly, 310 is not 306, we conclude the triangle is not a right-angled triangle.} \end{gathered}`

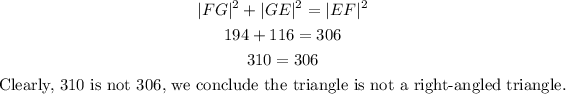
Hence, the correct answer is triangle EFG is not a right-angled triangle.