A Linear regression line has an equation in the form,
y= ax+b
where Y= Dependent variable
X= Independent variable
a= The intercept
b= The slope of the line.
So we are to get the summation of all the tables formulated.
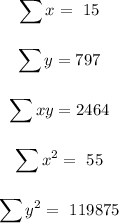
We are to solve for the mean of x, mean of y, a and b.
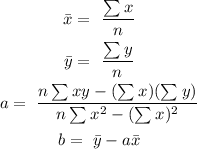
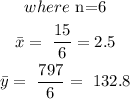
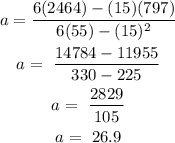
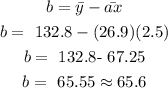
Hence the regression line equation is:
y=ax+b
y=26.9x+65.6
To find the projected profit of the year 2008, we would make use of the derived equation, y=26.9x+65.6
where x= 2008-1997= 11years,
y=?
Solving for y,
y= 26.9×11+65.6
y= 295.9+65.6
y= 361.15(thousand dollars) to the nearest thousand dollars
y= $361,000.
Hence the value for y= $361,000.