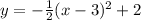We know that
• The vertex is (3,2).
,
• The x-intercept is at (1,0).
The vertex form of a parabola equation is-
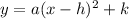
Where h and k are the coordinates of the vertex.
We use the given information to find the parameter a,
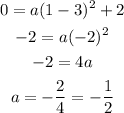
So, a is equal to -1/2.
We already have all the parameters to write the equation for the parabola in vertex form because h = 3, k = 2, and a = -1/2.