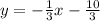Answer:
The equation of the line is;
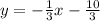
Step-by-step explanation:
Given that the line is perpendicular to the equation;
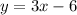
So, the slope of the line will be the negative inverse of the slope of the equation above;
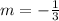
Also, the line passes through the point;

Applying the point-slope form of linear equation;

Substituting the values of the slope and coordinates;

Therefore, the equation of the line is;