Question

Can you help me solve the scale factor and center or dilation but simplified them as a fraction or whole number please

Answer 1

Hello!

Notice that the parellelogram E'F'G'H' is a dilatation of the parallelogram EFGH.

To obtain the scale factor, we can select two corresponding sides and divide the biggest by the smallest. Look:

`SF=(F^(\prime)G^(\prime))/(FG)`

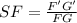
Notice that F'G' has 4 units in diagonal, while FG has 1 unit in diagonal. So:

`\text{ScaleFactor}=(4)/(1)`

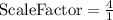
The scale factor is 4.

Center of Dilatation:

Note that we have only one point common to both parallelograms.

`H=H^(\prime)`

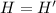
So, its coordinates are the center of dilatation (-5, -8).