Given,
The equation is
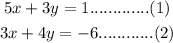
To find: Identify the systems with no solution and systems with infinitely many solutions.
Solutions: We will use the substitution method. After moving 3y to the right, we get:
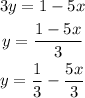
Substitute this in the second equation.
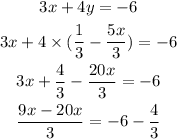
Further solved as,
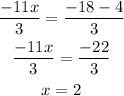
Put the value of x in equation (1)
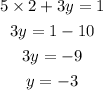
Thus, the value of x and y is (2,-3)