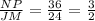1 Answer

Yershuachu · Answer 1 · 2023-01-25T22:58:09+0000

The addition of the three interior angles of a triangle is equal to 180°.

Considering triangle JMR, we get:

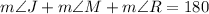
$m\angle J+m\angle M+m\angle R=180\degree$

Substituting with the data provided in the diagram:

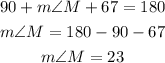
$\begin{gathered} 90\degree+m\angle M+67\degree=180\degree \\ m\angle M=180\degree-90\degree-67\degree \\ m\angle M=23\degree \end{gathered}$

Considering triangle KNP, we get:

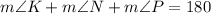
$m\angle K+m\angle N+m\angle P=180\degree$

Substituting with the data provided in the diagram:

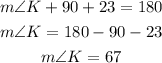
$\begin{gathered} m\angle K+90\degree+23\degree=180\degree \\ m\angle K=180\degree-90\degree-23\degree \\ m\angle K=67\degree \end{gathered}$

In consequence, the next angles are congruent:

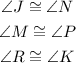
$\begin{gathered} \angle J\cong\angle N \\ \angle M\cong\angle P \\ \angle R\cong\angle K \end{gathered}$

Applying the AAA similarity theorem, then triangles JMR and NPK are similar.

A similarity ratio is the ratio of the lengths of the corresponding sides of two similar polygons.

The similarity ratio of triangle JMR to triangle NPK is:

$\begin{gathered} (JM)/(NP)=(24)/(36)=(2)/(3) \\ (MR)/(PK)=(26)/(39)=(2)/(3) \\ (JR)/(NK)=(10)/(15)=(2)/(3) \end{gathered}$

The similarity ratio of triangle NPK to triangle JMR is:

Please log in or register to add a comment.