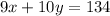Given:
1. A line has the equation 10x-9y=14.
2. The perpendicular line going through the point (6,8)
To determine the equation of the perpendicular line going through the point (6,8), we first get the slope of the given equation 10x-9y=14 as shown below:

Next, we note the rule:
For a line equation for the form of y=mx+b, the slope is m. Hence,
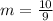
We also note that the perpendicular slope is the negative reciprocal of the given slope. So,
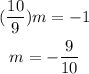
Then, we plug in m=-9/10, x=6, and y=8 into y=mx+b:
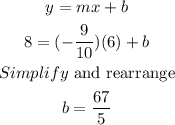
Now, we plug in m=-9/10 and b=67/5 into y=mx+b to find the equation:
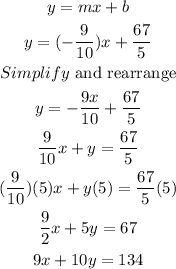
Therefore, the answer is: