Given:
There are given that the function:
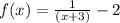
Step-by-step explanation:
The graph of the given function is shown below:
Now,
(1) Domain:
To find the domain of the given function, we need to find the value where the function is defined.
Then,
The domain of the given function is:
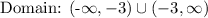
(2) Range:
To find the range of the given function, we need to find the set of values that correspond with the domain.
So,
The range of the given function is:
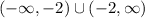
(3) Increasing on:
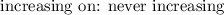
(4) Decreasing on:
The value of decreasing on:
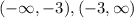
(5): All asymptote:
The value of asymptote are:
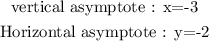
(6) All limit (4):
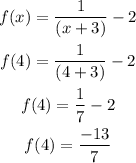
Hence, the all limit at 4 is -1.85.