Question

Use Direct Comparison Test to determine whether the series is convergent or divergent:

Answer 1

A series that has a finite sum is called convergent series. Otherwise, are divergent.

• Direct Comparison Test

Supposing that aₙ ≥ 0 and bₙ ≥ 0 for all values of n.

• Converges:, If aₙ ≤ bₙ for all values of n and

`\Sigma_(n=0)^(\infty)b_n`

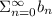
converges, then the series:

`\Sigma^(\infty)_(n=0)a_n`

also converges.

• Diverges: ,If aₙ ≥ bₙ for all values of n and

`\Sigma^(\infty)_(n=0)b_n`

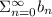
diverges, then the series:

`\Sigma^(\infty)_(n=0)a_(n)`

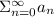
also diverges.

Our series:

`\Sigma_(n=0)^(\infty)(6+\sin(n))/(n^2)`

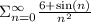
Applying the comparison we can see that the series converges.

Answer: converge.