Question

Use synthetic division to find the quotient. If there is a remainder do not include it in your answer. Recall:dividend\div divisor=quotient (6x^3-10x^2-7x-15) \div(x+1) Be sure to type your answer in descending powers of x with now spaces between your terms. Use the "^" key (shift+6) to indicate a power/exponent.Answer:

Answer 1

We have the next the next division

`(6x^3-10x^2-7x-15)/(x+1)`

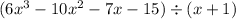
And we need to use synthetic division to find the quotient.

1. we must write the problem in a division-like format.

- we need to take the constant term of the divisor with the opposite sign and write it to the left. Then, we must write the coefficients of the dividend to the right.

2. we must write down the first coefficient without changes:

3. we need to multiply the entry in the left part of the table by the last entry in the result row and add the obtained result to the next coefficient of the dividend, and write down the sum.

4. We must continue the same process

5. We must continue the same process

Now, We have completed the table and have obtained the following resulting coefficients: 6. -16, 9 and -24

To identify the quotient we need all coefficients we obtained except the last coefficients which represents the remainder.

So, the quotient would be

`-6x^2-16x+9`

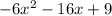
ANSWER:

-6x^2-16x+9