How much more will you have in your RRSP in 23 years if you start investing $1,100 at the end of each month now instead of waiting 3 years to begin contributing the same $1,100 at the end of each month? Interest is 6.6% compounded monthly.
Remember that
The formula for the future value of an ordinary annuity is equal to:
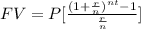
Part 1
start investing $1,100 at the end of each month now
we have
P=$1,100
r=6.6%=0.066
n=12
t=23 years
substitute in the given formula
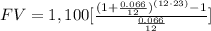
FV=$708,830.05
Part 2
waiting 3 years to begin contributing the same $1,100 at the end of each month
we have
P=$1,100
r=6.6%=0.066
n=12
t=20 years
substitute in the given formula
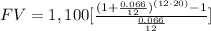
FV=$545,981.37
Part 3
Find out the difference
$708,830.05-$545,981.37=$162,848.68
therefore
the answer is $162,848.68