Question

Answer the 5 question at the bottom right side of the picture

Answer 1

We are asked to find out the measurement of the angles in the given figure.

Let us first identify those unknown angles

In the given figure, angle CBF and angle ADG are "Alternate Interior Angles"

We know that alternate interior angles are always equal so we can write

`\begin{gathered} \angle CBF=\angle ADG \\ 3x+16=5x-54 \\ 3x-5x=-54-16 \\ -2x=-70 \\ 2x=70 \\ x=(70)/(2) \\ x=35 \end{gathered}`

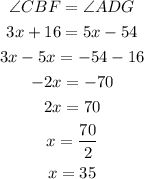
So the value of x is 35

Now we can find the exact values of angle CBF and ADG

`\begin{gathered} \angle CBF=3x+16=3(35)+16=105+16=121\degree \\ \angle ADG=5x-54=5(35)-54=175-54=121\degree \end{gathered}`

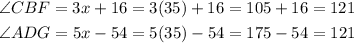
Therefore, angle CBF and angle ADG are equal to 121°

1) m ∠ABH

As you can see, angle ABH and angle CBF form a straight line angle which means that their sum must be equal to 180°.

`\begin{gathered} \angle ABH+\angle CBF=180\degree \\ \angle ABH+121\degree=180\degree \\ \angle ABH=180\degree-121\degree \\ \angle ABH=59\degree \end{gathered}`

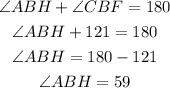
Therefore, angle ABH is 59°

2) m ∠GDF

In the given figure, angle ABH and angle GDF are "Corresponding Angles".

We know that corresponding angles are always equal.

Therefore, angle GDF is 59° since ∠GDF = ∠ABH

4) m ∠ABC

In the given figure, angle ABH and angle ABC are "Vertically Opposite Angles"

We know that vertically opposite angles are always equal.

Therefore, angle ABC is 59° since ∠ABC = ∠ABH

5) m ∠EDA

In the given figure, angle GDF and angle EDA are "Vertically Opposite Angles"

We know that vertically opposite angles are always equal.

Therefore, angle EDA is 59° since ∠EDA = ∠GDF

Summary:

1) ∠ABH = 59°

2) ∠GDF = 59°

3) x = 35°

4) ∠ABC = 59°

5) ∠EDA = 59°