Question

Preview Mode: Your score will not be recordedPoints (4, 5) and (10,5) are vertices of a rectangle.The length of the rectangle is twice the width.The other vertices are located at (4, ___) and (10,.). What could these ordered pairs be?a. Type your answers in the box.B1

Answer 1

(4, 7) and (10, -7)

Explanation

Given information

`\text{The vertices of a rectangle are (4, 5) and (10, 5)}`

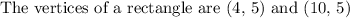
step 1: Find the distance between the two points using the below formula

`\begin{gathered} l\text{ = }\sqrt[]{(x1-x2)^2+(y1-y2)^2} \\ \end{gathered}`

From the given points, you will see that both coordinates lie on the same y-axis

Then, we can find the length as

`\begin{gathered} l\text{ = }\sqrt[]{(4-10)^2+(5-5)^2} \\ l\text{ = }\sqrt[]{(-6)^2\text{ + 0}} \\ l\text{ = }\sqrt[]{36} \\ \text{ = 6 units} \end{gathered}`

Since the length of the triangle is twice the width

Therefore, l = 2w

l = 2(6)

l = 12 units

The y-coordinate of the other vertices will be

y = 5 - 12

y = -7

Therefore, other vertices are

(4, -7) and (10, -7)