Question

an ordinary (fair) die is a cube with numbers 1-6 on the sides represented by painted spots.imagine that such a die is rolled Twice in succession and that the face Values of the 2 rolled are add together. this Sum is recorded as the outcome of a single trial of a Random experiment. compute the Probability of the events Event A) the Sum is Greater than 7Event B) the Sum is Divisible by 3

Answer 1

Given:

A die is rolled twice and the face values of the 2 rolls are added together.

The possible outcome for rolling a die twice is the sample space.

`n(S)=6*6=36.`

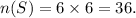
Event A) the Sum is Greater than 7

`A=\mleft\lbrace(2,6\mright),(3,5),(3,6),(4,4),\mleft(4,5\mright),(4,6),(5,3),(5,4),(5,5),(5,6)\}`
`n(A)=10`

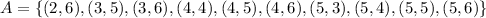
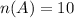
The probability is P(A).

`P(A)=(n(A))/(n(S))`

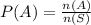
Substitute n(A)=10 and n(S)=36 in the equation, we get

`P(A)=(10)/(36)=(5)/(18)`

`P(A)=0.28`

The probability of event A is 5/18 or 0.28.

Event B) the Sum is Divisible by 3​

`B=\mleft\lbrace(1,2\mright),(1,5),(2,1),(2,4),(3,3),(3,6),(4,2),(4,5),(5,1),(5,4),(6,3),(6,5)\}`
`n(B)=12`

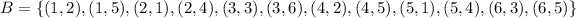
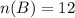
The probability is P(B).

`P(B)=(n(B))/(b(S))=(12)/(36)=(1)/(3)=0.33`

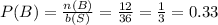
The probability of B is 1/3 or 0.33.