Given data:
* The initial velocity of the dart is 10.9 m/s.
* The angle of the initial velocity with the ground is 7.59 degree.
Solution:
The time period of the projectile motion is,
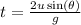
where u is the initial velocity, g is the acceleration due to gravity, and
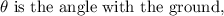
Substituting the known values,
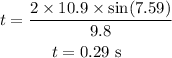
By the kinematics equation, the horizontal range of the dart is,
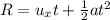
where u_x is the initial horizontal velocity, a is the acceleration, and t is the time of flight,
The acceleration of the dart is zero along the horizontal direction,
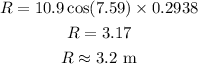
Thus, the distance traveled by the dart in the horizontal direction is 3.2 meter.
Hence, the dart can hit the target.