A triangle has 3 sides and 3 angles
Angles
B = 46 degrees (given)
C = 72 degrees
To find angle A
A + 46 + 72 = 180 (sum of angles in a triangle)
A + 118 = 180
A = 180 - 118
A=62
A = 62.0 degrees (to the nearest tenth)
Sides
a = 74 (given)
To find side b and c
We use sine rule

Therefore b = 60.3 (to the nearest tenth)
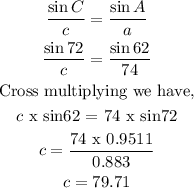
Therefore c = 79.7 (to the nearest tenth)