Substituting the second equation in the first one we get:
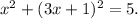
Simplifying the above equation we get:
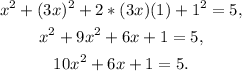
Subtracting 5 from the above equation we get:
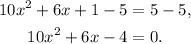
Now, notice that:
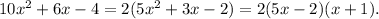
Therefore:
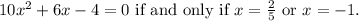
If x=2/5:

Therefore
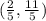
is a solution to the given system of equations.
If x=-1:
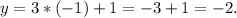
Therefore (-1,-2) is a solution to the given system of equations.
Answer: Third option.