Question

GHS has vertices (3.0.5.3 and 54 State the coordinates of the image of GHS after the transformation below D₂ o T(-3,1) Your answer

Answer 1

We have a triangle GHS which will be transformed by a dilation by a factor of 2, with center at (0,0) and a translation of (-3,1).

We can find the coordinates of a point (x,y) after the dilation of factor 2 as:

`P=(x,y)\longrightarrow P^(\prime)=(2x,2y)`

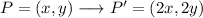
Then, the translation can be described as:

`P^(\prime)=(2x,2y)\longrightarrow P^(\prime)^(\prime)=(2x-3,2y+1)`

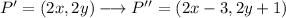
Then, for points G(3,1), H(5,3) and S(1,4), the transformations will result in:

`\begin{gathered} G=(3,1)\longrightarrow G^(\prime\prime)=(2\cdot3-3,2\cdot1+1)=(3,3) \\ H=(5,3)\longrightarrow H^(\prime\prime)=(2\cdot5-3,2\cdot3+1)=(7,7) \\ S=(1,4)\longrightarrow S^(\prime\prime)=(2\cdot1-3,2\cdot4+1)=(-1,9) \end{gathered}`

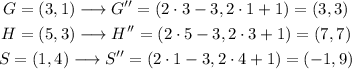
We can see the transformation in the graph as:

Answer:

Coordinates after the transformation:

G''=(3,3)

H''=(7,7)

S''=(-1,9)