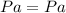ANSWER
The exponent of L must be 1
Step-by-step explanation
We have to write the dimensions of each variable in the equation. 8 and π are constants and have no units. The units of the variables, in the international system of units, are:
• Q = m³/s
,
• u = Pa·s
,
• r = m
,
• L = m
,
• P = Pa
Replace these into the equation. For this problem we can ignore the constants:
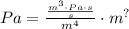
We want to have Pascal units on both sides for this to be dimensionally consistent. Note that the seconds in the numerator's fraction get cancelled:
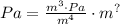
To have Pascal on both sides we need the same exponent in the meters. If we cancel m³ with m⁴, we have m¹ in the denominator:
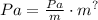
Now we can see that if L has exponent 1, then the units get cancelled correctly to obtain pressure units, as the equation shows.