Question

Solve the system of equations by ELIMINATION.4x - y = -45x = 2y+1Please assist with this

Answer 1

To answer this question, we need to rewrite the second equation as follows:

`5x=2y+1`

If we add -2y to both sides of the equation, we have:

`5x-2y=2y-2y+1\Rightarrow5x-2y=1`

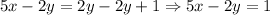
Now, we have the following equivalent system:

`\begin{cases}4x-y=-4 \\ 5x-2y=1\end{cases}`

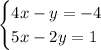
The main goal of the elimination method is to cancel one of the variables when we add or subtract the two equations.

To solve this system by elimination, we can multiply the first equation by -2 and then add the result to the second equation:

`-2(4x-y=-4)=-8x+2y=8`

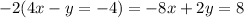
Then we have:

`\frac{\begin{cases}-8x+2y=8 \\ 5x-2y=1\end{cases}}{-3x+0y=9\Rightarrow-3x=9}`

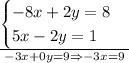
Now, if we divide both sides of the equation by -3, we have:

`-(3x)/(-3)=(9)/(-3)\Rightarrow x=-3`

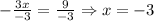
Therefore, x = -3.

To find the value of y, we can substitute the value of x = -3 into the first equation as follows:

`4(-3)-y=-4\Rightarrow-12-y=-4`

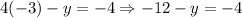
To find y, we can add 12 to both sides of the equation:

`-12+12-y=-4+12\Rightarrow-y=8\Rightarrow-1\cdot(-y)=-1\cdot8`

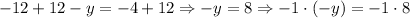
If we multiply by -1 to both sides of the equation, we have:

`y=-8`

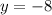
Therefore, the value for y = -8.

To check if both values are the solutions for the linear system of equations, we can substitute both values into the original equations as follows:

• x = -3

,

• y = -8

Then

`4(-3)-(-8)=-4\Rightarrow-12+8=-4\Rightarrow-4=-4_{}`
`5(-3)=2(-8)+1\Rightarrow-15=-16+1\Rightarrow-15=-15`

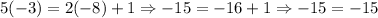
The results in both cases are true. Therefore, the solutions are correct.

In summary, we have that the solutions using the elimination method are x = -3, and y = -8.