Question

Question 1Given two equations of two different lines 4y=-3x+48 and 3 x+4y=-36a. Determine their slopesb.What is the relationship of these two lines?

Answer 1

`\begin{gathered} 4y=-3x+48 \\ 3x+4y=-36 \end{gathered}`

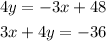
To determine the slope and the relationship of these two different lines, let's convert both equations to slope-intercept form first.

`y=mx+b`

where m = slope and b = y-intercept.

Let's convert the first equation first.

`\begin{gathered} 4y=-3x+48 \\ \text{Divide both sides by 4.} \\ (4y)/(4)=(-3x)/(4)+(48)/(4) \\ y=-(3)/(4)x+12 \end{gathered}`

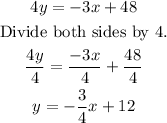
The slope of the first equation is -3/4.

Let's convert the second equation.

`\begin{gathered} 3x+4y=-36 \\ 4y=-3x-36 \\ \text{Divide both sides by 4.} \\ (4y)/(4)=(-3x)/(4)-(36)/(4) \\ y=-(3)/(4)x-9 \end{gathered}`

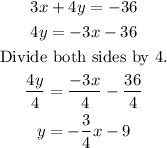
The slope of the second equation is also -3/4.

Since the slopes of the two lines are the same, they are parallel to each other. (relationship of the two lines)