Question

A time traveler can take 3 books with him, and he has 76 books to choose from. How many different ways can the books be selected?

Answer 1

We need to determine the combination of the 76 books taken 3 by 3. To do this, we have to use the following expression:

`C_(n,p)=(n!)/(p!(n-p)!)`

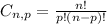
Where n is the number of elements in the group, p is the number of elements in the subgroup and C is the number of total combinations. So we have:

`\begin{gathered} C_(76,3)=(76!)/(3!(76-3)!) \\ C_(76,3)=(76!)/(3!(73)!) \\ C_(76,3)=(76\cdot75\cdot74\cdot73!)/(3!\cdot73!) \\ C_(76,3)=(76\cdot75\cdot74)/(3\cdot2\cdot1) \\ C_(76,3)=(421800)/(6)=70300 \end{gathered}`

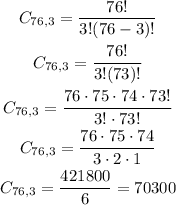
Thre are 70300 ways he can select the books.