Question

B. What is the mass of M1?C. What is the force Ft?

Answer 1

Given,

The mass m₂=9.00 kg

The acceleration of the crates, a=2.50 kg

The tension in the string that connects the two crates is, T=11.25 N

(b)

The tension in the string causes the mass m₁ to accelerate at the given acceleration. Thus from Newton's second law,

`T=m_1a`

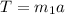
Thus, on substituting the known values,

`\begin{gathered} 11.25=m_1*2.5 \\ m_1=(11.25)/(2.5) \\ =4.5\text{ kg} \end{gathered}`

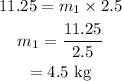
Therefore the mass m₁ is 4.5 kg

(c)

The total force applied is causing the two blocks to accelerate at the given rate. Therefore, from Newton's second law,

`F_T=(m_1+m_2)a`

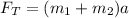
On substituting the known values,

`\begin{gathered} F_T=(9.00+4.50)2.50 \\ =33.75\text{ N} \end{gathered}`

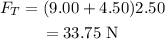
Thus, the total force applied to the crates is 33.75 N