Given statement is,
If two angles are complementary, then the angles are acute.
The converse statement is,
If there are two acute angles, then the two angles are complementary.
This is not always possible.
So, This statement is false.
Because,
Let us take two acute angles 20 and 40.
Then,
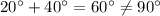
Hence, eventhough 20 and 40 are the acute angles, but they are not the complementary pair.
If we take two acute angles 60 and 30.
Then,
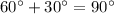
Hence, 60 and 30 are acute angles and the complementary angles too.