The answer is:
P U (Q n R) = {6, 7, 11, 12, 13, 15}
The question gives us 3 sets: P, Q and R and asks us to find:
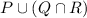
We should solve the sets in the bracket first because a bracket signifies relationship priority between sets Q and R comes before any relationship with P
Q n R means we are to find the intersection of Sets Q and R. This means that we should find which elements are present in both sets only.
If set Q contains {2, 7, 11} and set R contains {4, 7, 9, 11}
Therefore, the elements (or numbers) common to both sets are 7 and 11. Thus, this is given by:
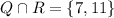
Now that we have established what is in the bracket, we can now proceed to explore the relationship with set P.
P U K is a union of sets P and K. This means that you can include all the elements (or numbers) of both sets P and K.
Therefore, we can solve P U (Q n R) as:
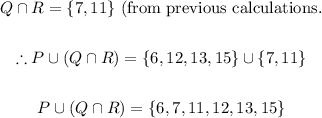
Therefore, the final answer is:
P U (Q n R) = {6, 7, 11, 12, 13, 15}