Question

It takes a printer 15hrs to print the class schedule for all of the students in college. A faster printer can do the jobs 9hrs. How long will it take to do the job if both printer are used?

Answer 1

Let's call T the total amount of material needed to print all the class schedules.

If the first printer takes 15 hours to finish printing all the schedules, that means it prints

`(T)/(15)`

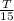
of the material per hour.

Similarly, since the second printer takes 9 hours to print all the material, then it prints

`(T)/(9)`

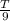
of the material per hour.

We con now propose an equation that will allow us to know how fast both printers working in tandem will finish printing all the material:

`x((T)/(15)+(T)/(9))=T`

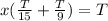
where x is the amount of hours it will take to print T. We begin by calulating what's inside the parentheses:

`x((T)/(15)+(T)/(9))=x((3T+5T)/(45))=x((8T)/(45))`

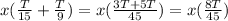
we now go back to the equation:

`x((8T)/(45))=T`

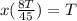
Dividing both sides by T,

`(8x)/(45)=1`

Multiplying both sides by 45,

`8x=45`

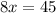
and finally, dividing both sides by 8,

`x=5.625`

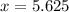
To end this question properly, let's remember that an hour has 60 minutes, so

`0.625h=37.5m`

and a minute has 60 seconds, so

`0.5m=30s`

All in all, it will take both printers 5 hours, 37 minutes and 30 seconds to finish printing the material.