Question

Evaluate. 5/6 + 1/3 × 5/8Write your answer in simplest form

Answer 1

The solution is;

`(25)/(24)\text{ or }1(1)/(24)`

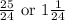
Step-by-step explanation:

We want to evaluate;

`(5)/(6)+(1)/(3)*(5)/(8)`

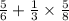
Firstly, we have to evaluate the multiplication;

`\begin{gathered} (5)/(6)+(1)/(3)*(5)/(8) \\ =(5)/(6)+(1*5)/(3*8) \\ =(5)/(6)+(5)/(24) \end{gathered}`

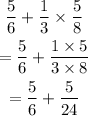
then we can now evaluate the addition ( According to the Order of BODMAS - Bracket Of Division Multiplication Addition and Subtraction)

`\begin{gathered} (5)/(6)+(5)/(24) \\ =(20+5)/(24) \\ =(25)/(24) \end{gathered}`

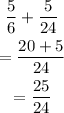
Therefore, the solution is;

`(25)/(24)\text{ or }1(1)/(24)`

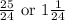
i provided the answer in both mixed fraction and improper fraction.