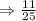Question

The mathematics faculty at a college consists of 7 professors, 8 associate professors, 6. assistant professors, and 4 instructors. If one faculty member is randomlyselected, find the probability of choosing a professor or an instructorThe probability is . (Type an integer or a fraction. Simplify your answer)

Answer 1

Let the number of professors be represented with the letter P

`n(P)=7`

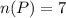
Let the number of associate professors be represented by the letter A

`n(A)=8`

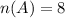
Let the number of assistant professors be represented by the letter S

`n(S)=6`

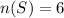
Let the number of instructors be represented by the letter I

`n(I)=4`

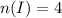
The total number of sample space will be calculated below as

`\begin{gathered} n(T)=n(P)+n(A)+n(S)+n(I) \\ n(T)=7+8+6+4 \\ n(T)=25 \end{gathered}`

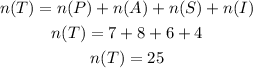
To figure out the probability of choosing a professor or an instructor, we will use the formula below

`Pr(PorI)=Pr(P)+Pr(I)`
`Pr(P)=(n(P))/(n(T))=(7)/(25)`
`Pr(I)=(n(I))/(n(T))=(4)/(25)`

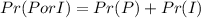
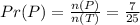
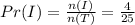
By substituting the values, we will have

`\begin{gathered} Pr(PorI)=Pr(P)+Pr(I) \\ Pr(PorI)=(7)/(25)+(4)/(25) \\ Pr(PorI)=(11)/(25) \end{gathered}`

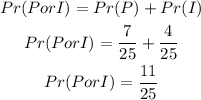
Hence,

The final answer is

`\Rightarrow(11)/(25)`