Question

In parallelogram HIJK, the measure of angle H is 45°.

Answer 1

Given:

`A\text{ parallelogram HIJK with the measure of angle H = 45 degr}ees`

The parallelogram can be sketched as shown below,

Part A:

To find the measure of angle J, we use the angle properties of a parallelogram.

1) The opposite interior angles are equal.

Hence,

`\begin{gathered} m\angle H=m\angle J \\ \text{Thus, }\angle J=45^0 \end{gathered}`

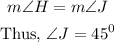
Therefore, the measure of angle J is 45 degrees.

Part B:

This is because the opposite interior angles of a parallelogram are equal.

Part C:

To find the measure of angle K, we use another angle property of a parallelogram.

2) The angles on the same side of the transversal are supplementary, that is, they add up to 180 degrees.

Hence,

`\begin{gathered} \text{Angle H and angle K lie on the same transversal. Hence, they are supplementary.} \\ \text{Thus,} \\ \angle H+\angle K=180^0 \\ \angle H=45^0 \\ 45+\angle K=180 \\ \angle K=180-45 \\ \angle K=135^0 \end{gathered}`

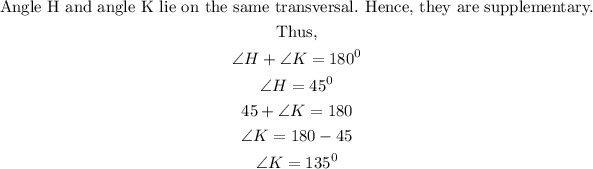
Therefore, the measure of angle K is 5 degrees.