Question

Boltzmann’s constant is 1.38066 × 10−23 J/K, and the universal gas constant is 8.31451 J/K · mol. If 3 mol of a gas is confined to a 4.2 L vessel at a pressure of 4.3 atm, what is the average kinetic energy of a gas molecule? Answer in units of J.

Answer 1

The average kinetic energy K of a sample of a monoatomic gas with temperature T is given by:

`K=(3)/(2)k_BT`

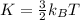
Where k_B is the Boltzmann's constant.

On the other hand, the pressure P, the volume V, the temperature T and the amount of substance n of an ideal gas are related through the Ideal Gas Law:

`PV=nRT`

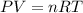
Where R is the Universal Gas Constant.

First, find the temperature T using the Ideal Gas Law. Then, replace the value for the temperature into the expression for the average kinetic energy to find its value.

To find T, isolate that variable from the Ideal Gas Law:

`T=(PV)/(nR)`

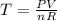
Replace P=4.3atm, V=4.2L, n=3mol and R=8.31451J/mol*K and convert the values to SI units when necessary to find the temperature T in Kelvin:

`T=((4.3atm*(101325Pa)/(1atm))(4.2L*(1m^3)/(1000L)))/((3mol)(8.31451(J)/(mol\cdot K)))=73.36K`

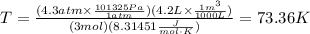
Use the value of T=73.36K to find the average kinetic energy of a gas molecule, assuming that it is a monoatomic gas:

`K=(3)/(2)k_BT=(3)/(2)(1.38066*10^(-23)(J)/(K))(73.36K)=1.52*10^(-21)J`

Therefore, the average kinetic energy of a gas molecule is 1.52*10^-21 J.