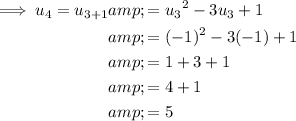Answer:
a) u₂ = 1
b) u₃ = -1
c) u₄ = 5
Explanation:
A recursive formula for an arithmetic sequence allows you to find the nth term of the sequence provided you know the value of the previous term in the sequence.
Given recursive rule:
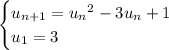
Part a
To find u₂, substitute n = 1 into the formula:
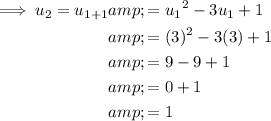
Part b
To find u₃, substitute n = 2 into the formula:
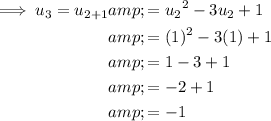
Part c
To find u₄, substitute n = 3 into the formula: