Question

Can you please help me

Answer 1

The line that represents the relationship between "y" and "x" passes through the origin and the points (k,7) and (-81,-9)

Assuming that "y" varies directly with "x", we can express their relationship as:

`y=mx`

Where "m" represents the slope of the line, also known as coefficient of proportionality or variation.

Using this expression and the known paired values (-81,-9) we can calculate the value of the slope as:

`\begin{gathered} -9=m(-81) \\ m=-(9)/(-81) \\ m=(1)/(9) \end{gathered}`

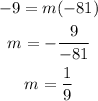
The slope of the line is m=1/9 → this value is constant, regardless the values of x and y. Using it you can determine the value of k as follows:

`\begin{gathered} y=(1)/(9)x \\ \text{For (k,7)} \\ 7=(1)/(9)k \\ k=(7)/((1)/(9)) \\ k=7\cdot9 \\ k=63 \end{gathered}`

The value of k is 63