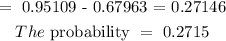Question

I need help with this question please a and b

Answer 1

Answer:
`X-N\text{ \lparen25200, 13500\rparen}`

The probability that a college student has between $31500 and $47550 is 0.2715

Step-by-step explanation:

Given:

The average student loan = $25200

The standard deviation = $13500

The distribution is normal

To find:

a) the distribution of X

b) the probability that the college graduate has between $31500 and $47550 in student loan

a) X = the student loan debt of randomly selected college graduat

To write the value of X and N in the formwritten:

The 1st parenthesis = average student loan = $25200

The 2nd parenthesis = standard deviation = $13500

`X-N\text{ \lparen25200, 13500\rparen}`

b) To get the probability that college student has between $31500 and $47550, we will apply the z-score formula:

`\begin{gathered} \begin{equation*} z=(X-μ)/(σ) \end{equation*} \\ X=\text{ value/score} \\ \mu\text{ = mean} \\ \sigma\text{ = standard deviation} \end{gathered}`
`\begin{gathered} when\text{ X = 31500} \\ z\text{ = }\frac{31500\text{ - 25200}}{13500} \\ z\text{ = 0.4667} \\ Using\text{ a standard normal table/calculator, the probability for z = 0.4667 is 0 67963} \end{gathered}`
`\begin{gathered} when\text{ X = 47550} \\ z\text{ = }\frac{47550\text{ - 25200}}{13500} \\ z\text{ = 1.6556} \\ Using\text{ a standard normal table/calculator, the probability for z = 1.6556 is 0.95109} \end{gathered}`

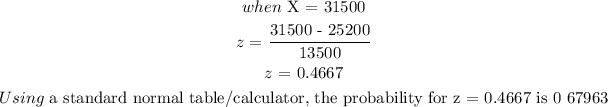
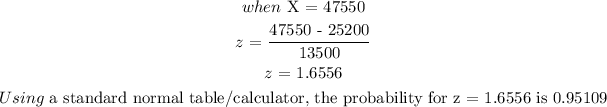
The probability that a college student has between $31500 and $47550 will be the difference in probability

`\begin{gathered} =\text{ 0.95109 - 0.67963 = 0.27146} \\ The\text{ probability }=\text{ 0.2715} \\ \end{gathered}`