The fair price to play the game is $23.61
Step-by-step explanation:
Number of singles = 5
number of fives = 8
Number of twenties = 4
number of $300 = 1
Total number = 5 + 8 + 4 + 1 = 18
fraction for each:
5/18 chance of getting singles
8/18 chance of getting fives
4/18 chance of getting twenties
1/18 chance of getting $300
We find the Expected values:
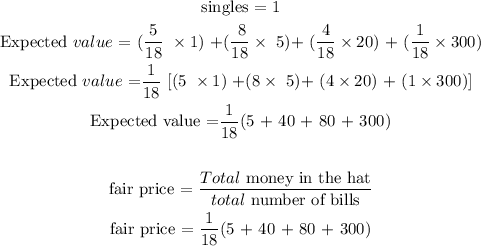

In the absence of further information, fair price is $23.61