Use the following formula for the amount of money obtained with a compounded interest:

where,
A: amount earnt = 6200
P: principal = 4700
r: interest rate in decimal form = 0.015
n: times at year = 2 (semiannually)
Replace the previous values of the parameters into the formula for A, simplify and solve for t by using properties of logarithm, as follow:
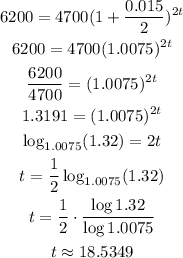
Hence, approximately 18.5349 years are necessary to obtain an amount of $6200