Given the system of equations:
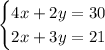
From the first equation, we have:
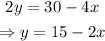
Using this result on the second equation:
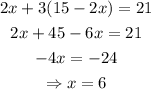
Then, the cost of 1 wrapping paper is $6.
We use this result to find y:
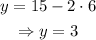
The cost of 1 greeting card is $3.
Part A:
The total cost of 1 wrapping paper and 1 box of greeting cards is:
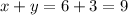
Answer: $9
Part B:
The order C is given by:
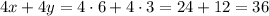
The total cost of order C is $36