Ok, considering that we have an angle, the measure of the adjacent leg, and we need to find the measure opposite leg. The most appropriate trigonometric ratio would be the tangent:
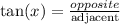
Replacing, we get:
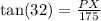
Clearing PX:
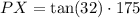
And operating:
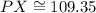
The distance PX is aproximately 109.35 meters.