Recall that the discriminant of a quadratic equation:
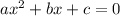
is:
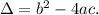
We know that:
1) If Δ=0 then the quadratic equation has one double root.
2) If Δ>0 then the quadratic equation has two different real roots.
3) If Δ<0 then the quadratic equation has two different nonreal roots.
Now, we can rewrite the given equation as follows:
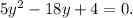
The discriminant of the above equation is:
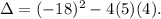
Simplifying the above result we get:
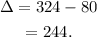
Since:
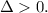
Then the given equation has two different real solutions.
Finally, notice that:
![\sqrt[]{244}=2\sqrt[]{61}](https://img.qammunity.org/2023/formulas/mathematics/college/1awviiz8g64bbq3m0jbrc6rwntln553a7n.png)
Therefore the solutions are both irrational.
Answer: Last option.